"Шпаргалки" по стереометрии

Видио материал по теме

 "Тела вращения. Цилиндр" 

https://prezi.com/view/Tk72q1xnL30mrDSOVqHA





Призма

            Призмой  называется многогранник, у которого две грани равные n-угольники (основания), а остальные грани - параллелограммы (боковые грани).

              Призма называется прямой, если все её боковые грани являются прямоугольниками.

• боковые ребра прямой призмы перпендикулярны основаниям
• высота прямой призмы равна боковому ребру

               Призма называется правильной, если она прямая, а ее основаниями служат правильные многоугольники.

Площадь поверхности и объем  призмы

Боковая поверхность  (прямой призмы)	Sбок =  Росн ∙ Н,   где Росн- периметр основания, Н- высота призмы
Полная поверхность  (любой призмы)	Sполн =Sбок + 2 Sосн
Объем    (любой призмы)	V =  Sосн ∙H,     где Sосн – площадь основания, Н- высота призмы

                                             Пирамида         

     Пирамидой называется многогранник, у которого одна грань – некоторый п- угольник (основание), а остальные грани треугольники с общей вершиной( вершина пирамиды).         

       Усеченной пирамидой называется часть пирамиды , заключенная между ее основанием     и сечением пирамиды, параллельным основанию.                                                                                              

       Высотой пирамиды называется перпендикуляр,проведенный из вершины пирамиды  к плоскости основания.                                                                                                                                     

       Диагональным сечением пирамиды называется сечение ее плоскостью, проходящей через два боковых ребра пирамиды, не лежащих в одной грани.

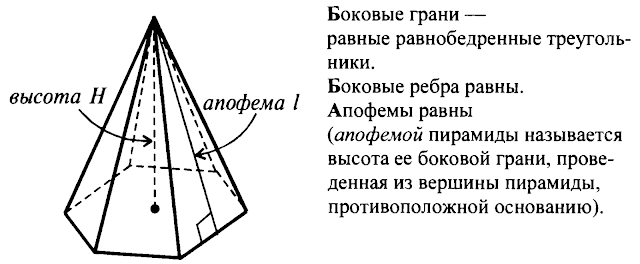
Правильная пирамида Пирамида называется правильной,   если ее основание – правильный п-угольник, а все боковые ребра равны.

Площадь поверхности и объем пирамиды

	Пирамида	Усеченная пирамида
Боковая поверхность (правильной пирамиды)	Sбок =  Росн ∙ L,  где  L- апофема	Sбок = (Р1 + Р2) ∙ L, где Р1и Р2- периметры оснований,  L- апофема
Полная поверхность (любой пирамиды)	Sполн =Sбок +  Sосн	Sполн = Sбок +  S1 + S2, где    S1  и S2-площади оснований
Объем (любой пирамиды)	V =  Sосн ∙H	V =  h (S1+ +S2) h-высота усеченной пирамиды